 题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
是n维线性空间V上的线性变换,证明:1)若在V的某基下矩阵A是某多项式d(λ)的友矩阵,则的最小多项
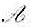 是n维线性空间V上的线性变换,证明:
是n维线性空间V上的线性变换,证明:
1)若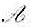 在V的某基下矩阵A是某多项式d(λ)的友矩阵,则
在V的某基下矩阵A是某多项式d(λ)的友矩阵,则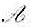 的最小多项式是d(λ);
的最小多项式是d(λ);
2)设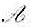 的最高次的不变因子是d(λ),则
的最高次的不变因子是d(λ),则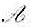 的最小多项式是d(λ)。
的最小多项式是d(λ)。
 答案
答案
 请输入或粘贴题目内容
搜题
请输入或粘贴题目内容
搜题
 拍照、语音搜题,请扫码进入小程序
拍照、语音搜题,请扫码进入小程序
 题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
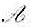 是n维线性空间V上的线性变换,证明:
是n维线性空间V上的线性变换,证明:
1)若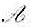 在V的某基下矩阵A是某多项式d(λ)的友矩阵,则
在V的某基下矩阵A是某多项式d(λ)的友矩阵,则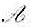 的最小多项式是d(λ);
的最小多项式是d(λ);
2)设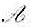 的最高次的不变因子是d(λ),则
的最高次的不变因子是d(λ),则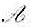 的最小多项式是d(λ)。
的最小多项式是d(λ)。
 答案
答案
 更多“是n维线性空间V上的线性变换,证明:1)若在V的某基下矩阵A是某多项式d(λ)的友矩阵,则的最小多项”相关的问题
更多“是n维线性空间V上的线性变换,证明:1)若在V的某基下矩阵A是某多项式d(λ)的友矩阵,则的最小多项”相关的问题
第1题
设![设是数域P上n维线性空间V的一个线性变换,证明:1)在P[x]中有一次数≤n2的多项式f(x),使2](https://img2.soutiyun.com/ask/2021-01-07/978874955275302.png) 是数域P上n维线性空间V的一个线性变换,证明:
是数域P上n维线性空间V的一个线性变换,证明:
1)在P[x]中有一次数≤n2的多项式f(x),使![设是数域P上n维线性空间V的一个线性变换,证明:1)在P[x]中有一次数≤n2的多项式f(x),使2](https://img2.soutiyun.com/ask/2021-01-07/978874992094408.png)
2)如果![设是数域P上n维线性空间V的一个线性变换,证明:1)在P[x]中有一次数≤n2的多项式f(x),使2](https://img2.soutiyun.com/ask/2021-01-07/978875015617754.png) ,那么
,那么![设是数域P上n维线性空间V的一个线性变换,证明:1)在P[x]中有一次数≤n2的多项式f(x),使2](https://img2.soutiyun.com/ask/2021-01-07/978875034333824.png) 这里d(x)是f(x)与g(x)的最大公因式;
这里d(x)是f(x)与g(x)的最大公因式;
3)![设是数域P上n维线性空间V的一个线性变换,证明:1)在P[x]中有一次数≤n2的多项式f(x),使2](https://img2.soutiyun.com/ask/2021-01-07/978874955275302.png) 可逆的充分必要条件是,有一常数项不为零的多项式f(x)使
可逆的充分必要条件是,有一常数项不为零的多项式f(x)使![设是数域P上n维线性空间V的一个线性变换,证明:1)在P[x]中有一次数≤n2的多项式f(x),使2](https://img2.soutiyun.com/ask/2021-01-07/978875092573155.png)
第3题
第5题
第6题
(I)求复数域上线性空间V的线性变换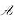 的特征值与特征向量,已知
的特征值与特征向量,已知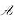 在一组基下的矩阵为:
在一组基下的矩阵为:
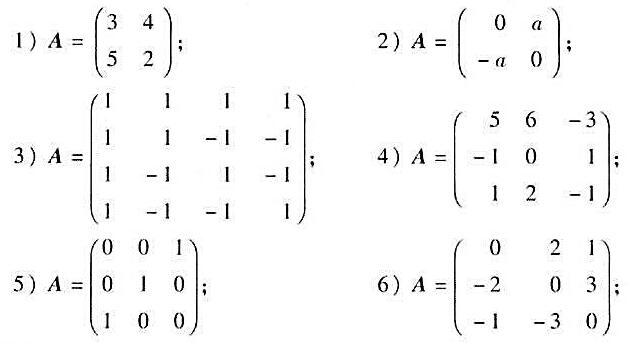
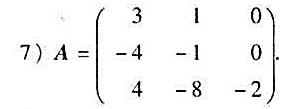
(II)在(I)中哪些变换的矩阵可以在适当的基下化成对角形?在可以化成对角形的情况,写出相应的基变换的过渡矩阵T,并验算T-1AT。
第7题
令V是实数域R上一个三维向量空间,σ是V的一个线性变换。它关于V的某一个基的矩阵是
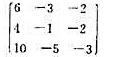
(i)求出σ的最小多项式p(x),并把p(x)在R[x]内分解为两个最高次项系数是1的不可约多项式p1(x)与p2(x)的乘积;
(ii)令Wi={ξ∈V|pi(σ)ξ=0},i=1,2。证明,Wi是σ的不变子空间,并且V=W1⊕W2;
(iii)在每一子空间Wi中选取一个基,凑成V的一个基,使得σ关于这个基的矩阵里只出现三个非零元素。
第10题
设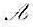 是欧氏空间V的一个变换。证明:如果
是欧氏空间V的一个变换。证明:如果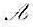 保持内积不变,即对于α,β∈V,
保持内积不变,即对于α,β∈V,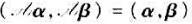 ,那么它一定是线性的,因而它是正交变换。
,那么它一定是线性的,因而它是正交变换。